1007. Числовая система Штерна-Броко

Дерево Штерна-Броко – это изящный способ построения множества всех неотрицательных дробей m / n, где m и n – взаимно простые числа. Идея состоит в том, чтобы начать с двух дробей (0/1, 1/0) и затем повторить нижеследующую операцию столько раз, сколько это нужно:

Вставить между двумя соседними дробями и

Например, первый шаг дает нам одно новое вхождение между 0/1 и 1/0:

0/1, 1/1, 1/0

Следующий шаг даст еще два:

0/1, 1/2, 1/1, 2/1, 1/0

Следующий шаг даст еще четыре:

0/1, 1/3, 1/2, 2/3, 1/1, 3/2, 2/1, 3/1, 1/0

Весь массив можно рассматривать, как бесконечное бинарное дерево, чьи верхние уровни выглядят так:

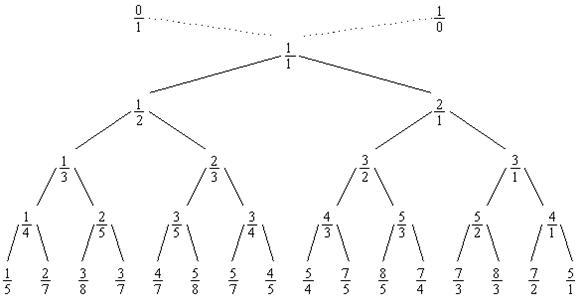
Эта конструкция сохраняет порядок, так что мы не можем получить одну и ту же дробь в различных местах.

Фактически мы можем рассматривать дерево Штерна-Броко как систему счисления для представления рациональных чисел, потому что каждая положительная, сокращенная дробь встречается в дереве только один раз. Будем использовать буквы L и R для обозначения того, двигаемся мы по левой или по правой ветви дерева, когда спускаемся от корня дерева к определенной дроби; тогда строка, состоящая из определенной последовательности этих L и R, уникальным образом определяет положение в дереве. Например, LRRL означает, что мы идем по левой ветви от 1/1 к 1/2, затем по правой к 2/3, затем по правой к 3/4, затем по левой к 5/7. Мы можем рассматривать LRRL как представление 5/7. Любая положительная дробь представляется таким путем уникальным строкой, состоящей из L и R.

Ну, скажем, почти любая дробь. Дроби 1/1 соответствует пустая строка. Мы будем обозначать ее I, так как это похоже на 1 и является первой буквой слова "identity" (единица).

В этой задаче вы должны представить данную положительную рациональную дробь в системе счисления Штерна-Броко.

Вход. Состоит из нескольких тестов. Каждый тест состоит из двух взаимно простых натуральных чисел m и n. Последний тест содержит две единицы и не обрабатывается.

Выход. Для каждого теста выведите в отдельной строке представление заданной дроби в системе счисления Штерна-Броко.

Пример входа	Пример выхода
5 7 878 323 1 1	LRRL RRLRRLRLLLLRLRRR

РЕШЕНИЕ

рекурсия

Анализ алгоритма

В задаче достаточно промоделировать при помощи рекурсии процесс построения дерева Штерна-Броко.

Пример

Найдем представление дроби 5/7 в системе счисления Штерна-Броко.

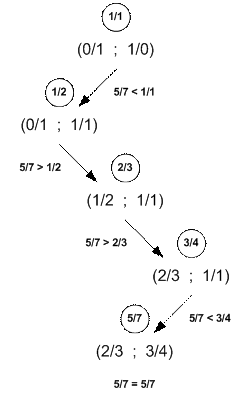
Представление дроби 5/7 имеет вид: LRRL.

Реализация алгоритма

Пусть искомая дробь m / n находится между дробями a1 / b1 и a2 / b2. В зависимости от того, лежит ли она правее или левее медианты (a1 + a2) / (b1 + b2), будем сдвигать левую или правую границу текущего интервала функции farrey.

void farrey(int a1, int b1, int a2, int b2)

{

if (n < b1 + b2) return;

if ((m == a1 + a2) && (n == b1 + b2)) return;

Выражение m / n < (a1 + a2) / (b1 + b2) эквивалентно m * (b1 + b2) < n * (a1 + a2).

if (m * (b1 + b2) < n * (a1 + a2))

printf("L"), farrey(a1,b1,a1+a2,b1+b2);

else

printf("R"), farrey(a1+a2,b1+b2,a2,b2);

}

Основная часть программы. Читаем входные данные. Запускаем функцию генерации всех дробей, начиная с (0/1, 1/0).

while(scanf("%d %d",&m,&n), !((m == 1) && (n == 1)))

{

farrey(0,1,1,0);

printf("\n");

}

Java реализация

import java.util.*;

public class Main

{

public static int m, n;

public static void Farrey(int a1, int b1, int a2, int b2)

{

if (n < b1 + b2) return;

if ((m == a1 + a2) && (n == b1 + b2)) return;

if (m * (b1 + b2) < n * (a1 + a2))

{

System.out.print("L");

Farrey(a1,b1,a1+a2,b1+b2);

}

else

{

System.out.print("R");

Farrey(a1+a2,b1+b2,a2,b2);

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(true)

{

m = con.nextInt();

n = con.nextInt();

if ((m == 1) && (n == 1)) break;

Farrey(0,1,1,0);

System.out.println();

}

con.close();

}

}